M系列をハッシュに

"当面C#と.NETな記録" さん（Hatena::Diary) のところに、興味深いエントリ「[C#] 一番右端の立っているビット位置を求める「ものすごい」コード」があったので、以下に引用：

一番右端の立っているビット位置(RightMostBit)を求めるコードで速いのないかなーと探していたら、ものっっっすごいコードに出会ってしまったのでご紹介。2ch のビット演算スレで 32bit 値のコードに出会って衝撃を受けて、その後 64bit 値版のヒントを見つけたのでコードを書いてみました。

...(中略)...

public static int GetNumberOfTrailingZeros( long x )
{
    ulong y = ( ulong ) ( x & -x );
    int i = ( int ) ( ( y * 0x03F566ED27179461UL ) >> 58 );
    return table[ i ];
}

table は以下のようにして求めます。

static int[] table;

table = new int[ 64 ];
ulong hash = 0x03F566ED27179461UL;
for ( int i = 0; i < 64; i++ )
{
    table[ hash >> 58 ] = i;
    hash <<= 1;
}

注: 引用元のコードには x==0 で分岐させる if 文があったが、それは筋が悪いので引用部分からは除去した。この改竄の結果、上掲のコードは、

引数 x の最下位ビットが 1、あるいは、 x==0 のいずれの場合でも、 GetNumberOfTrailingZeros() は 0 を返す　(★)

という仕様になった。

なるほど！

---

このアルゴリズムの主たる仕掛けは、次の (1)〜(3) だ。

(1) 有限体 上の6次多項式

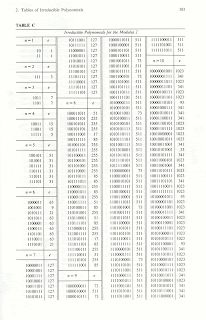
は原始多項式である（参照: 今回の記事の一番下の方にある、参考文献 [L&N1994] の表をスキャンした画像）。

(2) 一般に、 上の 次原始多項式を特性多項式とする非自明な無限数列は、M系列である（すなわち、周期 を持つ【この証明は、例えば [L&N1994] p.205 Theorem 6.33 にあるが、この事実を逆に原始多項式の定義と思っても構わない】)。

(3) 特性多項式が (1) である、次の線型漸化式と、その初期条件

で定まる 上の数列 を考える。 0 に引き続き、第 1 項 から第 項 までを順に並べ

とする。これを64bitの2進数とみなした 0x03F566ED27179461UL は、シフトを使ったハッシュに利用できる。

そういううまい話だ。

あったまいいなあ〜。M系列はこんな使い方もできたんだね。

---

でも、そういうことが分かると、元記事で挙げられている以外のマジックナンバーはないのかと気になる。

というのは、 上の6次原始多項式はこの世にたったの6個

しか存在しないからだ（[L&N1994] の表を参照してね）。

だから、2進数で表したときの先頭が 0000001... となる（要するに、★の性質を持つ）ことを、上記の原始多項式のそれぞれに対応する線型漸化式の初期条件として要請すれば、マジックナンバーが6通り（うち、3番目は既出）得られる:

0x0218A7A392DD9ABFUL
0x02FCA8CF75A6C487UL
0x03F566ED27179461UL
0x03C953422DFAE33BUL
0x03848D96BBCC54FDUL
0x03731D7ED10B2A4FUL

また、逆に、★の性質をもつ64bitのマジックナンバーは、この6通り以外には簡単に（システマティックに）求められるものは存在しない。

---

このエントリで用いた、「 上の全ての "既約多項式" とその "周期" を表にしたもの」の最初の部分が次の画像。（ただし、10 次既約多項式のリストは次のページに跨がっているので、この画像上では不完全。）

この画像は、文中でも参考文献として引いた、下記の本の p.385 をスキャンしたもの：

[L&N1994] R. Lidl and H. Niederreiter, Introduction to finite fields and their applications (Revised edition), Cambridge University Press, 1994.
ISBN978-0-521-46094-1

めちゃめちゃいい本です。絶対、おすすめ。（？！）

---
2009-07-12T01:40 追記: もし、128bit または 256bit、512bit のシフトがすばやい CPU とコンパイラをお使いなら、（★を満たし、かつ）"簡単に" に求められるマジックナンバーはそれぞれ 18 通りまたは 16 通り、48通りしかない。それぞれ 1 つずつを挙げておくと、

0x0106147916753E87126D6F634BB9957F

0x008E25C0C93720ADACB0FB7AE886C79CC5A452A7767BF4CD460EABE509FE178D

0x0042309CAB0DE9B9142B4FD925BF26A6603194697F458EB2CF1F741ADBB05AFAA814AF2EE073A4F5D448670BDB343BC3FE0F7C5CC8253B479F362A471B571311

こんなの誰も要らない？
2009-07-12T03:49 追記: 誤ったところを直しました。既に見た方、ごめんなさい。